董少南1,高 烈2,孙立海3,张敢生4,张宝忠5
（1.本溪市安达爆破工程有限公司，辽宁 本溪 117000；2.本钢集团公司，辽宁 本溪 117000，3辽宁隆烨爆破工程有限公司，辽宁 本溪 117000，4.辽宁科技学院，辽宁 本溪 117000，5.本钢矿山实业有限公司，辽宁 本溪 117000）
摘 要：阐述了最优化岩石爆破的理论和方法。提出了爆区的岩石最佳破碎原理、最优炸药单耗原理、能量平衡分配原理、可碎能带分布原理、单孔爆破最佳破碎原理和面能比中值化原理。并依据这些原理提出了如下爆破设计方法：按最优炸药单耗原理计算药量、按能量均匀度最大化原则布置炮孔、按综合能量梯度最大化原则安排起爆顺序、按可碎能带分布原理和单孔爆破最佳破碎原理设计装药结构及填塞方法。从而实现综合爆破危害效应最小、综合爆破效果最佳的目标。
关键词：最优化；岩石爆破；爆炸能量；爆能体
0 引 言
在岩石爆破中，炸药在岩体中爆炸所释放的能量，以爆炸应力波和爆轰气体膨胀压力的方式传递给岩石，使岩石产生破碎，但是真正用于破碎岩石的能量只占炸药释放能量的很少部分，大部分都消耗在产生爆破飞石、爆破震动、空气冲击波和噪音等有害效应方面。因此如何提高炸药的能量利用率，最大限度地改善岩石爆破效果具有非常重要的意义。
一般来讲，在实际工程爆破中综合考虑各种因素使总的爆破危害效应最小、总的爆破效果最佳的岩石爆破占绝大多数，因此是我们研究的重点内容。由于这类爆破是以综合爆破危害效应最小、综合爆破效果最佳为目标，因此我们把它称之为最优化岩石爆破。
1 最优化岩石爆破理论的基本内容
要想实现最优化岩石爆破[1]，必须解决以下三个方面的理论问题：一是如何布孔和起爆才能使整个爆区的岩石处于最佳破碎状态；二是如何选取炸药单耗才能使整个爆区的炸药能量利用率处于最佳状态；三是如何设计装药结构与填塞方式才能使每个炮孔的岩石破碎块度实现最优及炸药能量利用率达到最高。为了解决这三个问题我们提出了最优化岩石爆破理论，这个理论主要包括爆区的岩石最佳破碎原理、最优炸药单耗原理、能量平衡分配原理、可碎能带分布原理、单药包爆破岩石最佳破碎原理和面能比中值化原理。下面我分别对这几个基本原理的内容、提出的原因和依据、能够解决的问题进行阐述。
1.1 爆区的岩石最佳破碎原理
1.1.1 提出的原因和依据
（1）提出的原因
为了解决如何布孔和起爆才能使整个爆区的岩石处于最佳破碎状态问题，我们提出了爆区的岩石最佳破碎原理[2,3]。虽然在现有理论中也有一些关于布孔和起爆方面的理论，但是这些理论在客观上还解决不了这个问题。
（2）提出的依据
依据就是存在很多无法用现有理论给予合理解释的爆破现象，我们认为在这些现象背后一定隐藏着一个影响岩石爆破效果好坏的最本质规律，这个规律就是爆区的最佳破碎原理。
1.1.2 内容
根据爆破实践和道学原理，我们认为整个爆区的岩石最佳破碎原理是：在炸药和岩石一定的条件下，以综合效果为最优的岩石爆破中，爆区的岩石破碎效果与整个爆区的炸药能量分配均匀度、爆破过程中相邻炮孔岩石的综合能量梯度成正相关。因此每个爆区要想实现最优化爆破必须使炸药能量分配均匀度和爆破过程中相邻炮孔的岩石综合能量梯度值均达到最大化。这个原理就是整个爆区的岩石最佳破碎原理。要想实现最优化岩石爆破必须符合这个原理。
1.1.3 能量分配均匀度的概念
能量分配均匀度是指爆炸能量在整个爆区岩体中分布的均匀程度。
（1）爆能体与标准爆能体的概念
爆能体：是爆炸能量在岩体中各个方向传播的能量波波阵面所构成的空间结构体。
标准爆能体：是在标准布孔方式下，两个相邻且同时起爆的药包相切时的爆能体。
（2）爆炸能量分配均匀度的计算：
爆炸能量分布均匀度计算有绝对均匀度和相对均匀度的区别。计算方法和所起作用也略有不同。一个爆区孔眼布置的好坏，要综合考虑这两个参数。
（3）绝对均匀度的计算
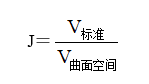
(1)
式中，J为爆炸能量分布的绝对均匀度；V标准为爆区内所有药包的标准爆能体所占据的空间体积；V曲面空间为爆区内与最外侧标准爆能体相切的曲面空间所围成的空间体积。
（4）相对均匀度的计算
相对均匀度的计算方法是：首先把爆区分解成若干个基本单元，针对每个基本单元计算它在标准药包布置方式下的绝对均匀度，并定为基准1；然后把实际布孔的绝对均匀度与标准布孔方式的绝对均匀度相比，所得比值就是此基本单元的相对均匀度。
1.1.4 能量梯度的定义及计算
所谓能量梯度就是指爆炸能量密度在单位距离上的变化量。
（1）能量梯度的计算
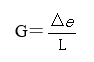
(2)
式中，G为能量梯度；△e为两相邻炮孔在同一瞬间能量密度的差值，根据能量密度变化曲线方程进行计算；L为炮孔间距。
1.1.5 爆炸能量密度的变化曲线
从微观上看每个药包的爆破过程都是一个由压应力为主向拉应力为主的转换过程。在这个过程中如果我们规定压应力为主的能量密度为正，拉应力为主的能量密度为负[4]。那么从宏观上看压应力为主的表现为向外膨胀，拉应力为主的表现为向内收缩。这样向外膨胀的能量状态就为正，向内收缩的能量状态就为负。因此爆破过程就可以看成是一个能量密度高低振荡的过程。这个过程可以用能量密度变化曲线方程表示，经验公式如下
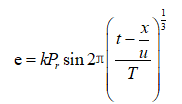
(3)
式中，e为能量密度；u为爆炸能量综合效应的传播速度；Pr为岩石中冲击波峰值压力；T为岩石破碎时间。
1.1.6 应用与解决的问题
爆区的岩石最佳破碎原理可以解决布孔和起爆的最优化问题。
（1）最佳布孔问题：
根据爆区的岩石最佳破碎原理，得出整个爆区的最佳布孔原则是能量分配均匀度趋向最大化。具体讲就是各炮孔的标准爆能体相切时达到最大化。
（2）最佳起爆问题：
根据爆区的岩石最佳破碎原理，得出爆区的最佳起爆原则是相邻炮孔的岩石综合能量梯度趋向最大化。具体来讲就是计算所有相邻炮孔在爆破时间内综合能量梯度最大值时的合理微差间隔时间与合理微差间隔距离，并据此确定合理的起爆网路。
1.2 最优炸药单耗原理
1.2.1 提出原因
当前最优炸药量的计算主要是根据利文斯顿最优爆破漏斗理论进行计算，但是这个计算结果与实际用量存在较大差距，因此在工程实际中根据利文斯顿最优爆破漏斗理论计算的值仅仅作为参考，更多的还是根据经验公式进行计算。所以为了解决最优炸药量的计算问题，我们提出了最优炸药单耗原理[5]。
1.2.2 内容
从实践中我们知道，炸药单耗过高则爆炸能量转变为飞石和空气冲击波的比例增加，而炸药单耗过低则爆炸能量转变为爆破震动的比例增加，只有炸药单耗在一个合适值时爆炸能量用于破碎的能量最高（即有用能量利用率最高），那么炸药单耗取何值时炸药的有用能量利用率最高呢？通过研究我们认为当爆破作用指数n＝0.5时炸药的有用能量利用率最高。关于这个结论可以从理论和实践两个方面得到证明。
1.2.3 理论证明
对于单个球形药包来说，我们把整个爆炸能量分成水平能量和垂直能量两部分，每部分再分成有用能量和无用能量两部分，我们再求当两部分有用能量乘积取最大值时的爆破作用指数n值，则结论即可得到证明。
设两部分有用能量的乘积为y，整个有用能量为1，水平方向有用能量为E∥有用，垂直方向有用能量E⊥有用。则列方程如下：
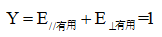
(4)
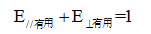
(5)
解得E∥有用＝E⊥有用＝1/2，对于单个球形药包的爆破漏斗来说，最小抵抗线W是垂直方向有用能量的量度，而爆破漏斗直径2r是水平方向有用能量的量度，二者相等既是爆破作用指数n＝0.5。因此当爆破作用指数n＝0.5时炸药的有用能量利用率达到最高。
1.2.4 药量计算
根据现有理论的体积公式
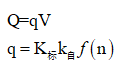
(6)
1.2.5 实践验证
依据上面的计算公式，我们可以根据各种岩石标准抛掷爆破的炸药单耗计算得到各种岩石松动爆破的炸药单耗。计算所得药量在实践中均能得到很好的松动爆破效果。
例如石灰石和铁矿石最优炸药单耗计算，按n＝0.5得到它的计算公式为q=0.475K标，对于石灰石K标＝1.0～1.2 kg／m3，铁矿石K标＝1.8～2.2 kg／m3，则其松动爆破时的最优炸药单耗值为：石灰石q=0.45～0.6 kg／m3，铁矿石q=0.85～1.05 kg／m3。而此值与实际需求相符。
1.3 能量平衡分配原理
1.3.1 提出的原因和依据
原因：是为了解决在爆破作用时间内爆破漏斗区域内爆炸能量的计算问题。
依据：就是存在很多爆破现象，表明爆炸能量在岩石中的分配与岩石在各个方向的阻力存在一定规律。这个规律就是能量平衡分配原理。
1.3.2 能量平衡分配原理的内容
所谓能量平衡分配原理就是在通过以爆源为原点的任何直线上，在爆破作用时间内分配的爆炸能量与此传播方向所受到的阻力乘积的矢量和总是为零。通过这个原理可以计算爆破漏斗范围内在爆破作用时间内所储存的爆炸能量和自由面系数的计算问题。
关于能量平衡分配原理可以从动量守恒定律得以证明。证明过程如下：
首先把整个爆炸能量E看作是由各个方向的能量单元e组成。每个能量单元e再分解成每个瞬间dt的能量de组成。由于每个de在以爆源为中心的一条直线上的能量分配与两个小球在以爆源为中心的直线上碰撞现象物理等效，因此爆炸能量在岩石中的传输问题可以看作是一种特殊形式的质点碰撞现象来加以解决。设e1为直线正向分配的能量，e2为直线负向分配的能量，e＝e1＋e2。则
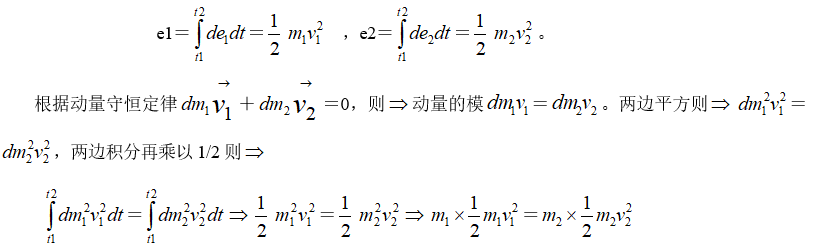
其中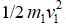
是在直线正向分配的爆炸能量e1，1/2
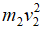是在直线负向分配的爆炸能量e2，
是爆炸能量在正向所扫过的岩石质量，它与爆炸能量在正向传输过程中所受到的阻力大小成正比，
是爆炸能量在负向所扫过的岩石质量，它与爆炸能量在负向传输过程中所受到的阻力大小成正比。乘以单位矢量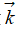
和－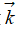
，所以在直线两个方向上的阻力分别为
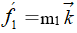和
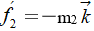。从而证得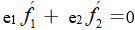
。
1.4 可碎能带分布原理
1.4.1 提出的原因和依据
原因：根据能量平衡分配原理，我们知道在爆破漏斗区域内有多少爆炸能量储存。那么这些能量又是如何分配的呢？因为这个问题不解决，我们就不知道何种分配状态有利于岩石破碎、何种分配状态不利于岩石破碎，因而也就不知道应当如何调整装药结构。所以为了解决这个问题我们提出了可碎能带分布原理。
依据：就是存在很多爆破现象，表明从爆源到自由面之间爆炸能量是分级分布的，其能量密度分布在数值上是不连续的；在空间上每级都是呈一定分布宽度的能带，而每条能带又都具有近似相同的能量密度，能带的能量密度从爆源到自由面依次呈等比级数降低。
1.4.2 可碎能带分布原理的内容
（1）可碎能带的形成：
炸药爆炸产生的能量以能量脉冲的形式在岩石中向外传播，由于能量脉冲在压实后的岩石中传播速度加快及遇到高能量密度区传播受阻将形成反射，因此就在岩石中形成一条条不同能量密度的能带在向外传播，在没有自由面的无限介质岩石中，裂隙区和弹性振动区处的能带能量密度分布在数值上呈连续性变化。相邻岩石质点之间仅有较小的变形，因此形成不了岩石破碎。而在有自由面的有限介质岩石中，由于能带在向外传播过程中遇到自由面传播受阻，因而就从自由面开始形成能量集聚，集聚的能量反射产生能量叠加形成更高密度能带。当其能量密度达到有自由面的岩石破碎强度时就形成第一条具备破碎条件的能带，我们称之为可碎能带。从爆源来的后续能量遇到第一条可碎能带后又将发生反射形成第二条可碎能带。这样就从自由面开始到爆源之间依次形成若干条可碎能带。这些可碎能带的能量密度分布在数值上呈间断性跳跃变化，这种间断性跳跃分布特性造成相邻岩石质点之间产生较大的剪切和拉伸变形，从而使岩石产生破碎。因此可碎能带的产生是岩石破碎的首要条件。
（2）可碎能带的分布：
空间上：可碎能带的空间分布状况可以用能带级数N、能带宽度B及能带的能量密度ei等参数进行描述。
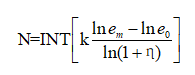
(7)
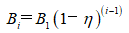
(8)
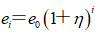
(9)
式中，k为修正系数；B1为第一条可碎能带宽度；η为相邻可碎能带的能量密度变化率，与岩石性质和最小抵抗线W相关；e0为岩石破碎所要求的最低能量密度；em为爆源在岩石中所产生的最高能量密度。
时间上：可碎能带在时间分布上是瞬时动态变化的。每条能带都有开始形成时间Tic、存留时间Til、岩石开始破碎时间Tiks和岩石结束破碎时间TiJs。对于单孔爆破来讲，可以通过调整这些参数来改善爆破效果，这几个参数如下：
第一条可碎能带形成时间T1c，也是第一条能带岩石开始破碎时间T1ks。T1c＝w/v＋△T1；
第一条可碎能带岩石结束破碎时间T1Js＝T1c＋△T1s；
最后一条可碎能带形成时间Tnc＝2w/v＋△Tn；
最后一条可碎能带开始消失时间Tnkx＝Tnc＋Tnl。此后可碎能带体系被破坏，如果此时爆破漏斗内岩石还未开始破碎，那么能量就以震动形式传走，不会形成岩石破碎。所以根据这几个参数关系可以推导出单孔爆破岩石最佳破碎原理。
1.4.3 单孔爆破岩石最佳破碎原理的内容
在单孔爆破[6,7]中，可碎能带的形成是岩石破碎的基础，岩石爆破效果的好坏与可碎能带的能量密度和时空参数密切相关，在实际爆破工作中主要通过调整第一条可碎能带岩石开始破碎时间T1ks、第一条可碎能带岩石结束破碎时间T1Js和最后一条可碎能带开始消失时间Tnkx来改善爆破效果。一般来讲有下列三种情况：
（1）当T1ks≥Tnkx时：爆破漏斗内岩石不能很好破碎，不能形成完整的可碎能带体系，因此也就不能形成爆破漏斗。
（2）当T1Js＜Tnkx时：爆破漏斗内岩石将产生过粉碎，过多能量将以爆破飞石动能、空气冲击波和噪音的形式传走。
（3）T1ks＜Tnkx≤T1Js时：能够形成完整的可碎能带体系，爆破漏斗内岩石能够得到很好的破碎，并形成完整的爆破漏斗，且当T1ks＜Tnkx＝T1Js爆破漏斗内岩石实现最佳破碎。
1.5 面能比中值化原理
1.5.1 提出的原因和依据
原因：在岩石爆破中，岩石为什么这样破碎而不那样破碎，是什么因素在控制岩石的破碎形状和数量，为了解决这个问题我们提出了面能比中值化原理。
依据：依据之一就是爆破岩块之间形状存在相似性的现象。这种现象表明有一种力量在支配岩石的破碎形状。这种力量就是面能比最小化原理。
依据之二就是在爆破漏斗内岩石是多级多块度破碎而不是单级单块度破碎。这种现象表明有一种力量在支配岩石的破碎数量。这种力量就是面能比最大化原理。
1.5.2 面能比中值化原理的内容
面能比中值化原理是由两个对立统一的原理组成，这两个原理就是面能比最大化原理和面能比最小化原理（即最小阻力原理）。所谓面能比中值化原理就是在由岩石和炸药组成的系统中，为了同时满足这两个对立统一因素阴阳相搏而取中道的一项破岩原理。因为岩石爆破就是由岩石和炸药所组成的阴阳对立统一系统，在这个系统中炸药为阳、岩石为阴。炸药爆炸能量向外发散，其特性是以最小的代价（即最小的破碎面积）获得最大的能量释放，因此爆炸能量总是沿着最小阻力方向开始释放，即遵循最小阻力原理，从面能比角度看它遵循的是面能比最小化原理。而岩石特性是以最小的代价（即以最小的岩石体积）捕获更多的爆炸能量（即获得最大破碎面积），因此它总是希望沿着最复杂的曲面形式进行破碎，从面能比角度看它所遵循的是面能比最大化原理。一般来讲，面能比最小化原理对岩块形状起主要作用，而面能比最大化原理对岩块形状起辅助作用。同时面能比最大化原理对岩块数量起主要作用，而面能比最小化原理对岩块数量起辅助作用。
（1）面能比最大化原理：
内容：所谓面能比最大化原理就是在爆破作用时间内，储存在某一岩石区域内的爆炸能量所造成的破碎面积与此区域内的爆炸能量之比总是趋向最大化。面能比可以按下式计算：
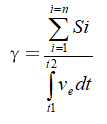
(10)
式中，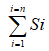
为爆破产生的破碎面面积总和；
为在破碎时间内储存在该区域岩石中的爆炸能量总和，其值可以根据能量平衡分配原理进行计算。
证明：因为从岩石破碎角度来讲，只要某区域内储存的爆炸能量密度达到岩石破碎所需的最小值，岩石就开始破碎。故有
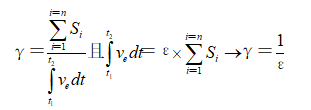
(11)
式中：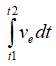
为在爆破时间内储存在该区域岩石中的爆炸能量总和，其值为定数；ε为岩石单位破碎面积所需的能量，对于特定岩石其值趋向
于单位破碎面积所需的最小值。
因为分子为定数、分母趋向最小值，所以对于特定岩石γ将趋向于最大化。
（2）最小阻力原理（面能比最小化原理）
内容：就是爆炸能量释放总是最先从最小阻力方向开始。从面能比角度看就是能量释放总是遵循产生的破碎面与释放能量之比趋于最小化。
证明：因为从能量释放角度来讲，爆炸能量总会沿着阻力最小路径释放，对于各向同性岩石就是沿着最小破碎面积释放。故有
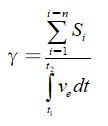
(12)
因为分子趋向最小值、分母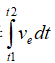
为常量，所以从能量释放角度看γ又将趋向于最小化。
2 应用技术研究
2.1 爆区设计评价方法
相对爆破效果指数：是用来判断不同爆破设计方案优劣的指标数。这个指数可以反映出同一爆区的不同爆破设计方案的优劣，指数高的爆破效果就好，指数低的爆破效果就差。它按下列公式计算：
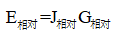
(13)
式中，E相对为相对爆破效果指数；J相对为整个爆破区能量分布的相对均匀度；G相对为整个爆区爆破过程中相邻炮孔的相对能量梯度。
2.2 装药结构设计和填塞方法
2.2.1 “主——辅药包”法的原理
由于爆破作用指数n＝0.5时的松动爆破可碎能带时间参数是T1ks＜Tnkx＜T1Js，但不符合单孔爆破最佳破碎T1ks＜Tnkx＝T1Js的条件。因此要想使n＝0.5时的松动爆破符合单孔爆破最佳破碎条件，必须通过增加爆源处可碎能带的存留时间（即增大Tnkx）或减少自由面处的可碎能带的结束破碎时间（即减小T1Js）。而增大Tnkx的途径可以通过增大最小抵抗线W和提高填塞质量获得。而减小T1Js的途径可以通过减小最小抵抗线W和改变装药结构获得。在爆破作用指数不变的情况下只能通过提高填塞质量和改变装药结构获得。为此我们提出“主——辅药包”装药爆破法[8]。辅助药包同时实现以下两个基本功能。一是起到引导岩石破碎的作用。二是起到提高填塞质量的作用。这就是“主——辅药包”装药爆破法的基本原理。
3 结束语
提出最优化岩石爆破理论的初衷，是为了解决如何进行爆破设计才能实现爆破危害效应最小、爆破有用效应最大的目标。为了实现这个目标，首先研究了应当如何布孔和起爆才能使爆区岩石达到最佳破碎状态问题，为此提出了爆区岩石最佳破碎原理。其次研究了应当如何计算药量才能使爆区炸药能量利用率达到最高问题，为此提出了最优炸药单耗原理。其三研究了应当如何设置装药结构和填塞方式才能使单个炮孔实现最优化爆破问题。
为实现单孔爆破的最优化首先必须解决岩石的破碎机理问题，而这个问题又归结为解决爆破区域内爆炸能量的计算、分配和释放形成岩块问题。为此首先提出能量平衡分配原理以解决爆破区域内爆炸能量的计算问题。进一步又研究爆破区域内爆炸能量的分配问题，提出可碎能带分布原理和单药包爆破最佳破碎原理。再进一步为解决如何形成岩块的形状和数量问题，又提出面能比中值化原理。
最后，根据上述原理得出实现最优化岩石爆破的最佳途径是：一、根据爆炸能量分布均匀度最大化原则布置炮孔。二、根据相邻炮孔的综合能量梯度最大化原则安排起爆网络。三、根据主辅药包法原则设置装药结构和填塞。
在长期的爆破实践中它基本上可以解决此类爆破现场出现的所有问题。客观地说这种理论更多地是来源于实践经验，而缺乏精确实验数据的支持，因此还有很多地方需要验证和深入研究。
参考文献
[1] 姚鹏.炸药与岩石的匹配分析研究[D].武汉理工大学,2011.
[2] 孔祥松,刘响钟,周纪军,等.岩石工程爆破破碎的机理研究[J].矿业研究与开发,2013,33(04):118-121.
[3] 卢海湘,廖明超.岩石爆破破碎机理的试验探讨[J].湖南有色金属,2001(06):6-8.
[4] 王永青,汪旭光.乳化炸药能量密度与爆破效果的关系[J].有色金属,2003(01):102-104.
[5] 刘慧,冯叔瑜.炸药单耗对爆破块度分布影响的理论探讨[J].爆炸与冲击,1997(04):72-75.
[6] 林发展,陈培煌,刘四德,等.钻爆法施工中单孔爆破的精细化数值模拟[J].工程爆破,2017,23(06):11-16.
[7] 李忠武,杨永英.岩石爆破松动破坏作用范围确定的探讨[J].工程爆破,1997(02):4-8.
[8] 刘义恒,刘先魁,林素彬.双层主、辅条形药包松动爆破起爆顺序的探讨[J].工程爆破,1997(03):60-64.