袁志华,杨 丽
(沈阳理工大学,辽宁 沈阳 110168)
摘 要:本文运用有限元软件ANSYS/LS-DYNA,围绕土介质爆炸扩腔过程的数值仿真研究展开。阐述土介质爆炸扩腔过程的数值仿真研究的背景和意义,国内外研究的现状,以及研究的主要内容和方案。其次叙述ANSYA/LS-DYNA的一些原理和炸药爆炸的理论基础。再次利用ALE算法和炸药爆轰产物的JWL状态方程,用ANSYS/LS-DYNA建立三维实体模型。用LS-PREPOST1.0进行后处理,可以观察到TNT炸药埋在土中不同深度时对应随时间的变化的压力、鼓包现象、轴向计算点的振速。还有作用炸药一个自由面与两个自由面对应随时间变化的压力、鼓包现象、径向计算点的振速。通过观察压力变化可以看出土介质爆炸扩腔的过程。
关键词:数值模拟;压力;膨胀现象;振动速度;膨胀腔
NUMERICAL SIMULATION ANALYSIS OF TNT EXPLOSION UNDER DIFFERENT DEPTHS OF SOIL BASED ON ANSYS/LS-DYNA
YUAN Zhihua,YANG Li
(Shenyangligong university Liaoning,Shenyang 110168,China)
Abstract:The paper basic on the vast literature, using the relatively mature finite element software ANSYS/LS-DYNA, and researching around the numerical simulation of process of Soil medium blast expand cavity.Firstly, state the underground and meaning of researching for process of soil medium blast expand cavity, the current research at home and abroad, and the main contents and solutions.Secondly,express some theories of ANSYS/LS-DYNA and explosive.Lastly, use the ALE method and the JWL state equation of explosive outcome,and use ANSYS/LS-DYNA to establish the three-dimensional entity model. Use LS-PREPOST1.0 for post-processing, the pressure, bulge, and the vibration velocity of radial calculations of TNT over time while acing on different depth and the same time on one and two free surfaces can be observed. And the process of soil medium blast expand cavity can be seen through observing pressure change.
Key words:numerical simulation, pressure, bulge phenomenon, vibration velocity, expand cavity
0 引 言
随着科学技术迅猛发展,土中爆炸技术在军事和国民经济建设中越来越显示出巨大作用。在军事领域,利用装药土中爆炸可以快速开挖单兵掩体,压缩爆破构筑坑道工事同时研究弹药土中爆炸载荷对人防工事作用也是函待解决的问题。在民用领域,开挖渠道、开采矿藏、修路造田、定向爆破筑坝也广泛应用土中爆炸技术。目前,解决工程中很多实际问题,以经验设计为主,理论研究和实验研究与实践需要还相差甚远,至今尚未建立起合适的土中爆炸作用理论模型。随着有限元技术的飞速发展,运用计算机进行数值模拟越来越广泛地应用于常规的爆炸领域。从广义上讲,计算机模拟本身就可以看作一种基本试验。计算机计算弹体的侵彻与炸药爆炸过程以及各种非线性波的相互作用等问题,实际上是求解含有很多线与非线性的偏微分方程、积分方程以及代数方程等的耦合方程组。本文利用ANSYS/LS-DANY软件在数值仿真方面的应用,对炸药在土介质不同深度和作用炸药不同自由面进行仿真模拟研究;然后把炸药在土中不同深度的压力、鼓包现象、轴向振速进行比较,作用炸药不同自由面的压力、鼓包现象、径向振速进行比较;得出具有一定参考意义的结论。
1 爆炸的理论基础
装药爆轰后,爆轰产物的压力达几十万大气压,直接与炸药接触的土石受到强烈的压缩,结构完全破坏,颗粒被压碎。整个土石因受爆炸产物挤压发生径向运动,形成一个空腔,成为排出区,排出区的体积约为装药体积的几十倍甚至几百倍。与排出区相临接的是强烈压碎区。在此区域内原土石结构全被破坏和压碎,并且在均质岩土中能观察到细密的裂纹。
随着与爆炸中心的距离的增大,爆炸产物的能量将传给更多的介质,爆炸波在介质内形成的压缩应力波幅迅速下降。当压缩应力值小于土石的动态抗压强度极限时,土石不再被压坏和压碎,基本上保持原有的结构。
1.1 连续介质力学基本方程
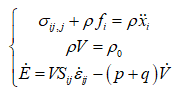
(1)
式中, 为Cauchy应力张度;
为Cauchy应力张度;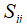 为Cauchy偏应力张量;
为Cauchy偏应力张量;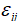 为应变率张量;
为应变率张量; 为体积力;
为体积力;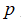 为静水压力;
为静水压力;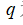 为体积粘性力;
为体积粘性力;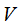 为变形梯度;
为变形梯度;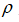 为介质当前密度;
为介质当前密度;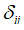 为Kronecker符号;
为Kronecker符号;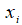 为现时构型下加速度。
为现时构型下加速度。
1.2 土介质本构方程
土介质的屈服函数为
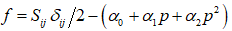
(2)
式中,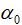 为常数;
为常数;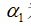 为常数;
为常数;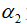 为常数;
为常数;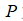 为压力。
为压力。
在实验研究数据基础上得到![]() 与体积应变的关系为:
与体积应变的关系为:
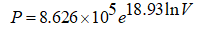
(3)
1.3 炸药爆轰产物状态方程
本论文采用了JWL状态方程,其形式为:
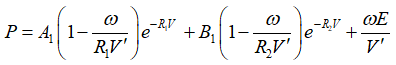
(4)
式中,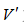 为相对体积;
为相对体积;![]() 为单位体积炸药内能;
为单位体积炸药内能;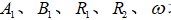 均为JWL状态方程参数。
均为JWL状态方程参数。
对于装药密度为1.2 g/m3的TNT炸药,各相关参数分别取值如下:A=741 GPa,B=18 GPa, =0.35,R1=5.56,R2=1.56,
=0.35,R1=5.56,R2=1.56,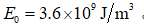 。此外,炸药的爆速D=5500 m/s爆压
。此外,炸药的爆速D=5500 m/s爆压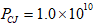 Pa。
Pa。
1.4 定界条件
初始条件为:
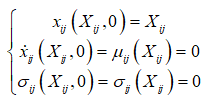
(5)
其中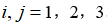 。边界条件为:在土介质与大气之间有常压存在。炸药爆炸作用过程中,土介质与爆炸产物之间满足:
。边界条件为:在土介质与大气之间有常压存在。炸药爆炸作用过程中,土介质与爆炸产物之间满足:
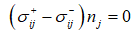
(6)
2 炸药在土中不同深度爆炸压力变化过程的数值模拟
2.1 建立有限元模型
由于问题的对称性,为了节省计算时间只建立1/2个模型,考虑到爆炸作用后形成空腔的经验尺寸,取计算区域为140 cm×70 cm×190 cm的矩形体,三种情况下炸药中心位于自由表面以下20 cm、25 cm、30 cm处,计算中的炸药区域尺寸取80 cm×5 cm×10 cm。建立有限元分析模型如下图1所示,图中PART1、PART2和PART3分别为土体、炸药以及空气单元模型。
对有限元模型进行正确的约束,使模型符合数值模拟要求,利用ANSYS/LS-DANY大型分析软件进行有限元分析。

分别建立炸药在土介质中深度20 cm、25 cm、30 cm的有限元模型,在所有约束加载完成后,进行求解。
2.2 炸药埋在土中三种不同深度的压力结果分析
以下为炸药在土中深度20 cm、25 cm、30 cm的不同时刻的压力分布图。
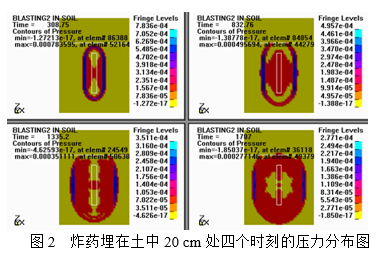
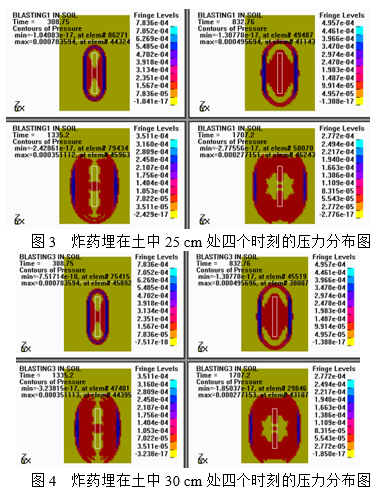
由以上四个时刻的压力分布可知随着t的增加,最大压应力峰值迅速减小,在t=1335.2 μm此时土中应力波在装药正上方受到自由面影响。在该区域由于稀疏波作用,应力场由压应力变为拉应力,装药正上方质点开始向上运动,应力场分布受稀疏波扰动开始发生变化。在t=1335.2 μm和t=1707.2 μm两个时刻土介质最大主应力分布图可知,自由面稀疏作用已经到达空腔的上表面,稀疏波所到之处,应力场分布规律均有较大改变。在t=1707.2 μm时自由面稀疏波已经越过空腔到达下表面,并对土中很大区域内传播的应力波产生影响,使空腔表面的应力场分布变得十分复杂,这会使空腔表面的运动产生微弱波动。模拟结果显示,柱状药包在不同深度压力较为接近,同时向上下两端扩散。
3 炸药埋在土中不同深度爆炸鼓包现象与轴向计算点振速分析
以前面模型为基础,建立相同的有限元分析模型,利用ANSYS/LS-DANY软件进行分析。
3.1 炸药埋在土中三种不同深度的鼓包现象分析
以下分别为炸药埋在土中深度20 cm、25 cm、30 cm的的鼓包现象分析图。如下图所示。


由上面的三个图可以看出炸药离自由面越近的鼓包现象越明显,受自由面稀疏波作用,装药正上方土介质加速运动,两侧土壤也逐渐开始隆起即形成了鼓包运动,越靠近自由面,越先接触稀疏波,随着时间的增加,稀疏波作用区域越大,鼓包现象越明显。
3.2 炸药埋在土中三种不同深度的轴向计算点的振速分析
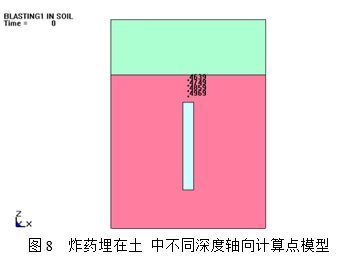
以下分别为炸药埋在土中深度20 cm、25 cm、30 cm的的轴向计算点的振速分析图如下所示。
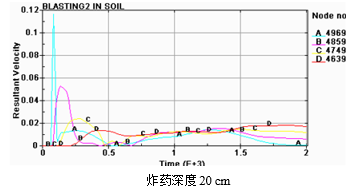
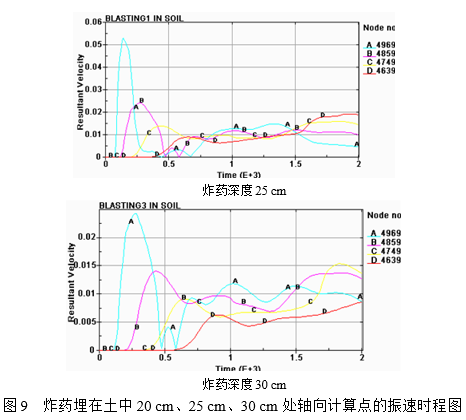
由图可以看出炸药深度25 cm时,土介质各节点振速在500 μs前变化特别大,说明在500 μs之前是一个快速的发展过程,在500μs之后各节点的振速变化不大,而在图9中可以看出土介质各节点振速在700 μs前变化比较大,在700 μs之后各节点的振速变化不大,看出土介质各节点振速在750 μs前变化比较大,在750 μs之后各节点的振速变化不大。说明炸药离自由面越近相同的土介质节点越先振动,而且振动的越激烈。由以上三幅图还可以看出炸药离自由面越近振速的峰值越大。
综上所诉,炸药埋在土中的深度离自由面越近,爆破效果越好。
4 结 论
通过用ANSYS/LS-DYNA软件对本论文建立三维实体模型、进行数值模拟。到炸药在土中不同深度对应随时间的变化的压力、鼓包现象、轴向计算点的振速。得出以下结论:
炸药离自由面越近,应力场越先发生变化,因为土中应力波在装药正上方受到自由面影响,在该区域由于稀疏波作用,应力场由压应力变为拉应力,装药正上方质点开始向上运动,应力场分布受稀疏波扰动开始发生变化。炸药离自由面越近,鼓包现象越明显,而且对应的轴向计算点的振速峰值越大。作用炸药两个自由面的压力比作用炸药一个自由面的变化均匀,比作用炸药一个自由面的鼓包现象明显,比作用炸药一个自由面的径向计算点的振速峰值。
参考文献:
[1] 田宏伟.框架结构在地下爆炸冲击下的动力响应研究[D].长安大学,2007.
[2] 国胜兵,赵毅,赵跃堂,等.地下结构在竖向和水平地震荷载作用下的动力分析[J].地下空间,2002(04):314-319+371.
[3] 国胜兵,王明洋,赵跃堂,等.爆炸地震波作用下地下结构动力响应数值分析[J].世界地震工程,2004(04):137-142.
[4] 梁霍夫.岩土中爆炸动力学基础[M].刘光寰,王明洋,译.工程兵工程学院.1993.
[5] 叶序双.爆炸作用基础(第2版)[M].南京:解放军理工大学出版社.2001.
[6] 张建华,裴来政.敞口耦合装药爆炸扩腔数值模拟[J].爆破,2005(01):34-37.
[7] 顾文彬,叶序双,詹发民,等.球形装药半无限土介质中爆炸动力学分析[J].工程爆破,1999(01):5-10.
