董英健1，贾建军2，郭航伸1
（1.辽宁科技大学矿业学院，辽宁 鞍山 114051；2.鞍钢矿业爆破有限公司，辽宁 鞍山 114051）
摘 要：介绍一种爆破振动信号处理方法—微分经验模态分解（Differential Empirical Mode Decomposition，DEMD），并结合多宝山铜矿选矿厂中碎车间基础爆破振动监测试验，与经验模态分解（Empirical Mode Decomposition,EMD）进行对比分析爆破振动信号的频率筛分、混叠失真情况以及分解后信号的功率谱特性。结果显示：与EMD相比，DEMD有效得抑制信号混叠失真现象，且从信号的功率谱变化特征得出DEMD将不同的优势频率分量提取出来，爆破振动信号频率筛分效果优越于EMD方法。
关键词：采矿；爆破振动；信号分析；微分经验模态分解
Comparision between Differential Empirical Mode Decomposition and Empirical Mode Decomposition of blasting vibration signals
DONG Yingjian1，JIA Jianjun2，GUO Hangshen1
（1. School of Mining Engineering，University of Science and Technology LiaoNing，Anshan 114051；2. Ansteel mining blasting Co.,Ltd LiaoNing，Anshan 114051）
Abstract: A new analysis methods of blasting vibration signals namely differential integral empirical mode decomposition(DEMD) was proposed .The comprehension of frenquency sieving，aliasing distortion and the power spectrum characteristic of decomposition signals was explored combining blasting vibration monitoring experiment by EMD and DEMD。The results show that aliasing distortion was controlled and different frequency components were extracted from the power spectrum of the signals by DEMD comparied with EMD method .The conclusion indicates that DEMD is superior than EMD method at certain aspects.
Key words: mining，blasting vibration，signals analysis，DEMD
0 引 言
为了满足我国经济建设发展需要，露天矿山持续地进行大规模的开发，工程爆破技术广泛地应用于矿山生产建设中，爆破破岩是露天矿开采过程中主要破岩方法。在露天台阶深孔爆破过程中，爆破振动对周围的构筑物以及露天矿的边坡的影响是无法避免的，已然成为了环境公害之一[1]。国内外很多学者通过对爆破振动信号的特征分析来对爆破振动效应展开了深入研究。针对CEEMD和TQWT组合的信号精细化特征提取方法，杨仁树等[2]指出对爆破振动信号的分析不依赖于先验小波基的选择，实现了信号的二次滤波，抑制了杂波分量对信号特征的干扰，提取了复杂环境下的爆破振动信号特征信息，为爆破振动信号的分析与处理提供了有利依据。
Kai Du等[3]描述了爆破振动信号的非平稳性，提出了广义维度算法，为爆破振动信号进一步的研究与分析提供了新的方法。郭涛等[4]将频率切片小波变换算法引入到了爆破振动信号时频特征分析中，克服了传统EMD分解时频理论中的缺陷，对信号的滤波起到积极作用。YAN等[5,6]提出了一种新的时频分析方法—频率切片小波变换，弥补了小波分析准确性取决于小波基函数的不足，对信号的局部特征进行准确性评价，对爆破振动信号分析具有重要的意义。
从以上的爆破振动信号处理方法来看，大部分方法首先是对信号进行分解，但分解的方法不同，对后期的爆破振动分析结果也有差异，因此，研究爆破振动信号的分解方法具有重要意义。以某铜矿二期选矿厂中碎车间基础开挖为工程背景，开展了爆破振动监测试验，分别采用EMD和DEMD两种方法对监测的爆破振动信号进行分解，并分析信号的频率筛分、混叠失真情况以及分解后信号的功率谱特性，处理结果可为爆破振动信号的分析提供参考。
1.1 经验模态分解理论
EMD与传统的小波变换相比，分解结果并不依赖小波基的选择，因为EMD以监测信号的本身时间尺度来分解，将信号分解成若干个本征模态函数（Intrinsic Mode Function，IMF）。其分解步骤如下[7,8]：确定爆破振动信号S(t)上的所有极大值点、极小值点，并采用三次样条函数对极大值点、极小值点进行插值，连接极大值点、极小值点来拟合上、下包络线，其中检查上下包络线是否将信号数据涵盖，避免遗漏信号重要数据信息；令包络线的均值定义为m1,考虑h11=x(t)-m1，若h11满足极值点的数量与过零点的数量相等或至多相差1且关于时间轴对称，则停止，假如不满足，进行k次重复计算，直到h1k满足其条件，则s(t)的第一个本征模态函数记为c1=h1k.将r(t)=s(t)-c1(t)作为新的信号，重复以上过程，获得本征模态函数c2，c3，……，cn，若rn成为单调函数，则停止。s(t)分解为多个本征模态函数及rn的和，即：s(t)=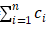
(t)+rm(t)。
1.2 微分经验模态理论
DEMD算法在进行EMD处理前先对原始爆破振动信号进行微分处理，然后再对每一阶IMF分量进行积分。通过对原始信号进行微分，改变了信号中不同频率成分所占比重，增强 EMD的频率分解能力，进一步改善END的模态混叠现象[9]。DEMD算法的步骤如下[10]：(1)对原始爆破振动信号x(t)进行一次微分得到x1(t),对x1(t)进行EMD算法处理，求取分解后IMF分量的功率谱,判断分解后的k个IMF分量是否有模态混叠现象。若存在，再次对信号x(t)进行微分处理，然后用EMD方法来分解微分后的信号，一直到经过n次微分处理再进行EMD分解求出的Cni(t)分量不存在模态混叠现象为止，rno(t)为分解过程中残余分量。(2)将各IMF分量Cni(t)做一次积分处理得: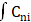
(t)dt=b(n-1)i(t)+b(n-1)io,然后对各b(n-1)i(t)进行EMD分解得到：b(n-1)i(t)=c(n-1)i(t)+r(n-1)i(t)；(3)c(n-1)i(t)是原信号x(t)微分（n-1）次得出的IMF分量，那么它剩下的信号为：r(n-1)0（t)=
+
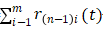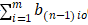(4)不断进行步骤(2)~(3)，直到n次积分后得到原信号的每一阶IMF分量及其残余信号分量，此时原始的信号能够表示成：X(t)=
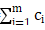(t)+rm(t)式中rm(t)
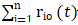代表残余分量。
对比两种算法的基本理论，两者都是从高频到低频依次将信号分解出来，获得具有单频函数的本征模态分量，但对于爆破振动信号来说，由于外界复杂因素较多，EMD法在分解过程高频部分分量不能完全被分解，并从下一阶段提取一部分频率，导致本阶段频率掺杂其他成分，出现混叠失真现象，若要抑制此情况发生，应提高振幅比来改善EMD效果[11,12]，而对爆破振动原始信号进行微分处理，正好达到提高振幅比的目的，提高信号频率筛分效果。
2.1 工程环境与地质条件
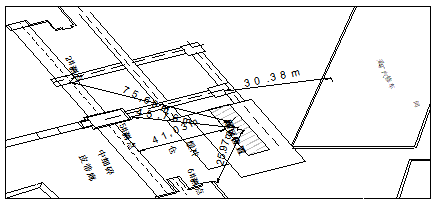
本工程位于一期选矿厂中细碎皮带廊以东、采矿汽车修理厂以西地段，施工范围长南北约40 m、东西宽约20 m。本次爆破位于施工区域东侧，距东边的采矿汽修车间最近处约30 m，距南边一期中细碎车间最近处约26 m，距西边的中细碎皮带廊最近处约41 m，距西北边的筛分皮带廊30 m以上。爆区周边环境及测点布置如图1所示。
图1 爆区周边环境及测点布置图
根据爆区周边已开挖断面推测，其岩性应为硬质碎屑岩。无地表水，推测无地下水或有少量地下水。为了有效控制爆破振动和爆破飞石，考虑距离本爆区最近的中细碎车间受到振动的影响，防止爆破可能产生的飞石超出20 m范围，本工程采用微差爆破技术，每个炮孔装药量为12 kg，孔内分两段进行间隔装药，其中下段药量为7.2 kg，间隔堵塞长度为0.7 m，上段药量为4.8 kg，上堵塞长度为3.4 m。布孔方式采取矩形布孔，孔内分段装药，斜线起爆网络，孔内采用400 ms导爆管雷管，地表采用17 ms、25 ms、42 ms和65 ms导爆管雷管连接，实现逐孔起爆。爆破参数如表1。（孔内微差？）
表1 车间基础开挖爆破参数
本次爆破开挖测试仪器采用中科院成都测控有限公司生产的TC-4850测振仪，对周围的建筑物的质点速度进行监测。本次工程选择了3个测点，出于对周围车间安全稳定性的考虑，将5#测点布置在爆区西北边的筛分皮带廊上、6#测点布置在爆区南边的中细碎车间、2#测点布置在爆区北边的公路附近。具体布置方法如下[13]：首先将待测点的位置处理干净，然后将石膏涂在测点上，最后把传感器紧紧地贴在测点。并且使传感器X指向爆源方向，Y指向水平切向，Z指向竖直方向。监测数据如表2所示。
表2 爆破监测数据
2.3 DEMD与EMD对比分析
通过对现场的爆破振动监测以及数据整理可以得到2#测点、5#测点、6#测点的三个方向的爆破振动信号原始波形图，如图4所示。
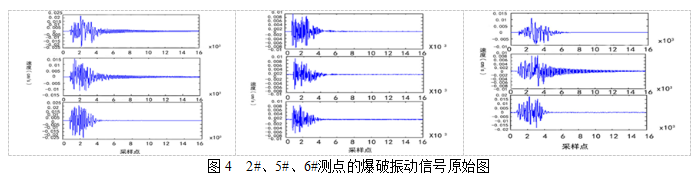
5#测点在进行爆破振动监测过程中，由于受到周围环境因素的影响，信号中掺杂着较多非真实成分，对爆破振动信号进行处理之前，需要对原始信号作进一步处理，消除信号掺杂的噪声，尽可能的还原信号的真实形态[14]。
信号的去噪方法多采用小波消噪，小波分析具有时频局部化特点，对于非平稳信号而言，小波能够有效的区分信号的真实特征和噪声。小波消噪过程如下[15]：小波消噪时前提条件必须选择一个小波基，然后对5#爆破振动原始信号进行小波变换，采用相关方法对小波系数进行处理，最后通过小波逆变换得到了已消除噪声的爆破振动信号波形。5#测点的振动波形图经过去噪后如图5所示。
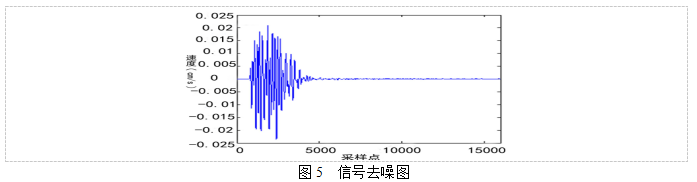
5#测点振动信号经过小波去噪后，应用信号处理软件编制程序对中细碎皮带廊监测的振动信号分别进行EMD与DEMD分解，如图6、图7所示。
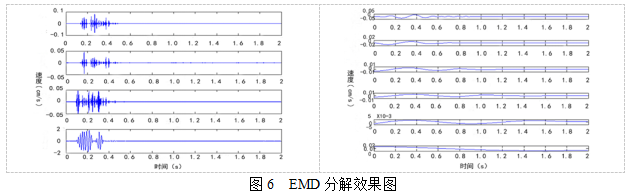
对比图6、图7的分解结果：EMD处理爆破振动信号时依靠自身时间尺度来分解，通过原始爆破振动信号与包络线的平均值之差并不断筛选已达到终止条件来确定单频的本征模态函数分量，对于此次监测得爆破振动信号来说，通过EMD方法将监测的爆破振动原始信号分解成10个本征模态函数分量，IMF1～IMF4在分解初期出现模式混叠现象，且本征模态函数分量中极值点与零点的数目不一致（或至多相差1），这是因为在分解过程中高频部分不能完全被分解以至于提取下一阶段频率来补充，导致高低频率混在同一阶段，同时还掩盖部分高频分量，另外通过IMF2、IMF3和IMF4分量的情况来看，信号的能量逐渐增加，振幅呈增强趋势。IMF10分量显示了信号的变化趋势趋于稳定状态表明了这是由于监测仪器的漂零所引起的。与EMD相比，DEMD首先对爆破振动原始信号进行微分处理，然后对每一个本征模态函数分量进行积分，从分解的结果图得出，将信号共分解成13个本征模态函数分量，将EMD不能分解的高频部分再次分解高频、低频分量，并且使得每一个本征模态函数分量符合单频函数的条件，消除每一个本征模态函数分量的混叠现象，克服EMD对高频分量分解不彻底的局限性。
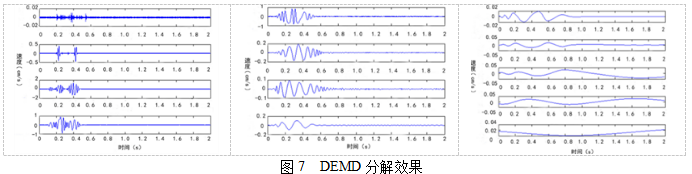
图8为EMD与DEMD分解后的功率谱图，可以得出爆破振动原始信号在EMD分解过程中，每个能量所对应的频率量无法识别出来，而且部分优势频率分量被遗漏，频率筛分的效果不明显，降低了信号的处理精度，这是因为EMD在处理信号过程中起初对信号进行了三次样条插值并没考虑分解出来的本征模态函数是否符合单频函数的条件与混叠失真现象，然而从DEMD处理的功率谱可以得到，通过对爆破振动原始信号进行微分处理，判断出不同频率分量所占比重，DEMD方法在频率识别方面优越于EMD，对爆破振动信号分析处理具有积极的意义。其次振动信号通过DEMD方法的处理，分解出的爆破振动信号功率谱特征变化较大，但大部分频率都在200 HZ以下，与EMD方法相比，DEMD方法使能量所对应的优势频率分量得以体现，提高了信号频率分辨能力。
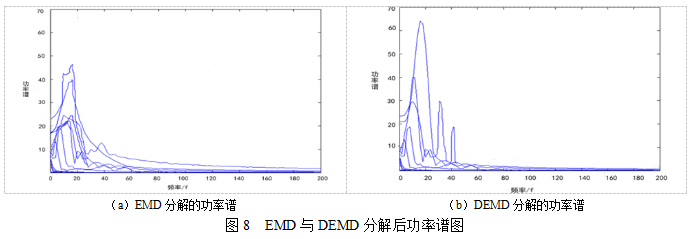
3 结 论
（1）DEMD算法以EMD为基础，对中碎车间爆破振动原始信号进行微分计算，改变信号中不同频率成分所占比重，将EMD没有分解出的本征模态函数分量IMF5～IMF8分解出来，与EMD相比，该方法抑制了每一个本征模态函数分量中的混叠失真现象。
（2）通过DEMD处理得爆破振动信号功率谱可得，该方法能识别出较高能量所对应的部分优势频率分量，在信号频率的筛分能力方面优越于EMD方法，有利于对爆破信号能量的进一步分析。
参考文献：
[1] 中国生,熊正明.基于小波包能量谱的建(构)筑物爆破地震安全评估[J].岩土力学,2010,31(05):1522—1528.
[2] 杨仁树,付晓强,杨国梁,等.基于CEMMD与TQWT组合方法的爆破振动信号精细化特征提取[J].振动与冲击,2017,36(03):38-44.
[3] Kai Du,Xiang Fang. Generalized dimension based on morphological covering for blasting vibration signal processing[J].Earth and Environmental Science,2017.
[4] 郭涛,方向,谢全民.频率切片小波变换在爆破振动信号时频特征精确提取中应用[J].振动与冲击,2013,32(22):73－78.
[5] YAN Z,MIYAMOTO A,JANG Z,et al. An overall theoretical description of frquency slice wavelet transform[J].Mechanical System & Signal Processing,2010,24(02):491-507.
[6] YAN Z,MIYAMOTO A,JANG Z.Frquency slice algorithm for model signal separation and damping identification[J].Computer & Structure,2011,89(01)：14-26.
[7] 孙强,王梦晓,徐玉山,等.岩巷爆破振动信号HHT分析与应用[J].工程爆破,2016,22(01):1-7.
[8] 李鹏,卢文波,陈明,等.高地应力环境下梯段爆破诱发振动特征的试验研究[J].工程爆破,2011,17(01):1-7.
[9] 景蓓蓓,李鸿光.基于微分的经验模式方法在转子裂纹和碰摩故障诊断中的应用[J].噪声与振动控制,2009.5(01):66-69
[10] 季艳.基于时频分析旋转机械故障特征提取方法研究[D].燕山大学,2015.
[11] 沈国际,陶利民,陈仲生.多频信号经验模态分解的理论研究及应用[J].振动工程学报,2005(01):96-99.
[12] Feldman M.Analytical basics of the EMD:Two harmonics decomposition[J].Mechanical Systems and Signal Processing,2009, 23(07):2059-2071.
[13] 李继业,蒲朝钦,何兴贵.节理岩体边坡爆破振动衰减特征分析[J].爆破,2018,35(02):32-36+113.
[14] 李鹏,卢文波,乔新明,等.岩石高边坡开挖爆破振动信号处理与振动响应分析[J].煤炭学报,2011,36(S2):401-405.
[15] 邓青林,赵国彦.基于EEMD和小波的爆破振动信号去噪[J].爆破,2015,32(04):33-38.